Note: All comments and opinions expressed on "MATLAB for everyone" are mine alone and do not necessarily reflect those of my employers, past or present.

본 포스팅은 아래의 MathWorks 김종헌 프로님의 Path Planning 시리즈 중 아래의 비디오를 정리한 것입니다.

이 포스팅은 모바일 패스 플레이닝 시리즈의 세번째 파트의 네번째 시간으로 Navigation toolbox에서 제공하는 path planning algorithm 중 최적화 기반 경로 계획 방법에 대해 알아본다.

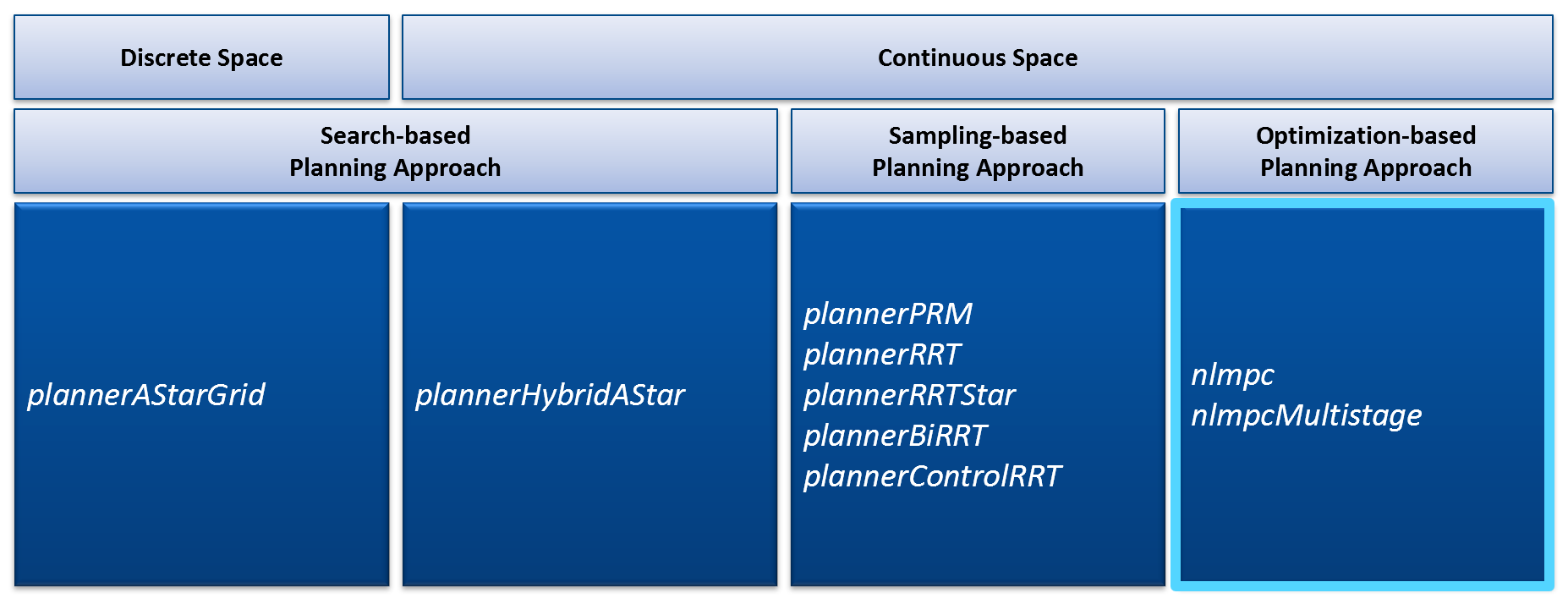
그림 1. Path Planning 알고리즘의 구분과 이번에 알아볼 Optimization-Based Path Planning 알고리즘

경로 계획 알고리즘의 분류에 대해 알고 싶은 사람은 시리즈 첫 번째 포스팅을 참고하시기 바란다. 그림 1 표의 가장 오른쪽의 설명과 같이 MATLAB에서 제공하는 최적화 기반 경로 계획 방법은 MPC, 즉 model predictive control을 이용하는 방법이다.

Model Predictive Control (MPC)

MPC solves a constrained optimization problem over a moving time horizon

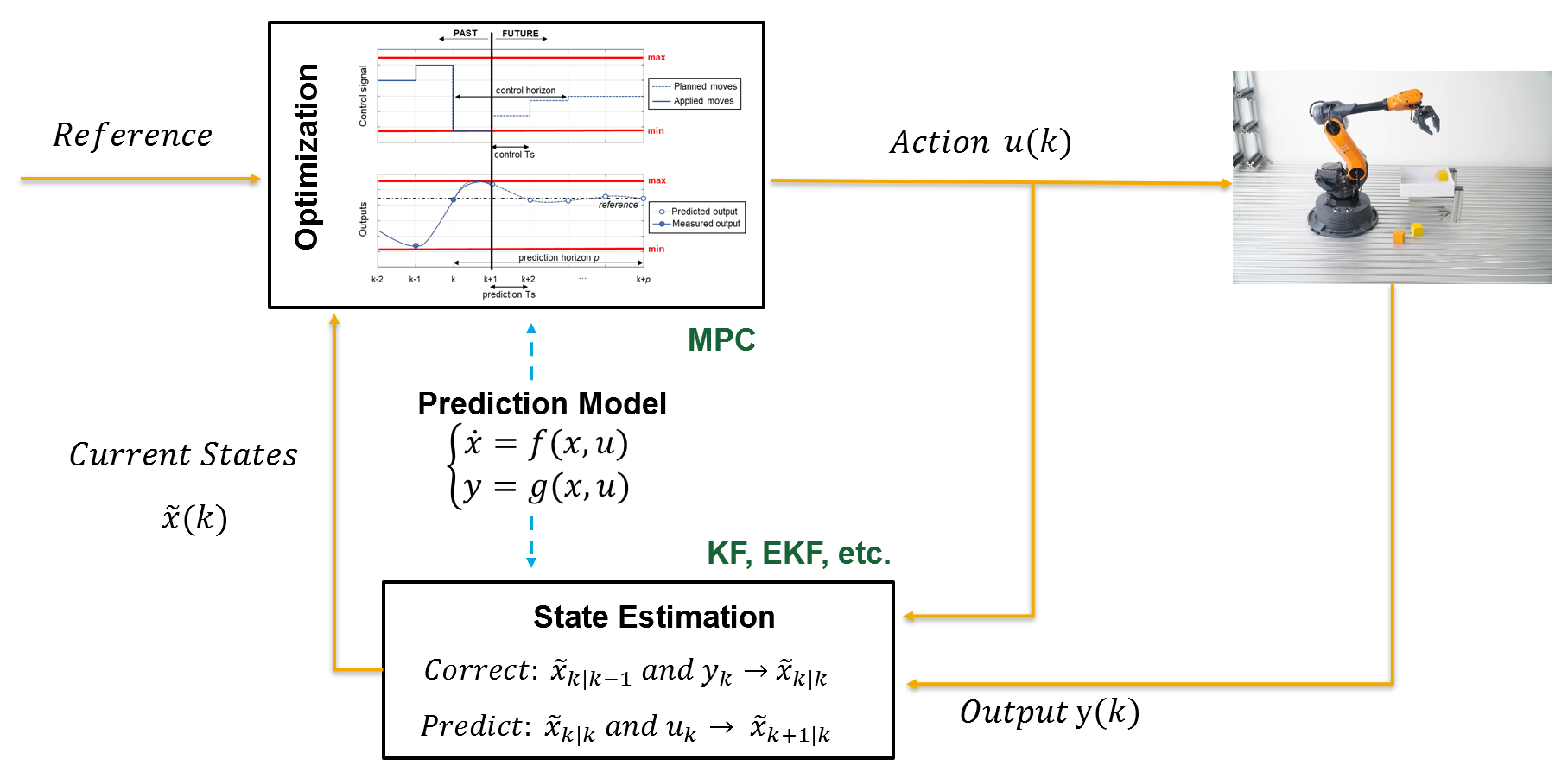
그림 2. MPC의 작동 방법 개요

MPC는 제어 목표를 비용 함수로 인코딩하고 이를 최소화하는 제어 신호를 입력 및 출력 제약 조건에 따라 생성한다.

Model predictive control이라는 이름에서도 알 수 있듯이 제어하려는 프로세스의 내부에 모델이 있고, 이 모델은 최적화 프로세스에서 미래에 일어날 가능성이 있는 일을 “예측”하는데 사용된다. MPC는 피드백 컨트롤러이기 때문에, 모델이 실제를 아주 정확하게 예측하지 않더라도 피드백을 통해 에러를 어느 정도 수정할 수 있으므로 예측 모델이 완벽할 필요는 없다.

How does MPC work?

그럼 실제로 MPC가 어떻게 동작하는지 살펴보자.

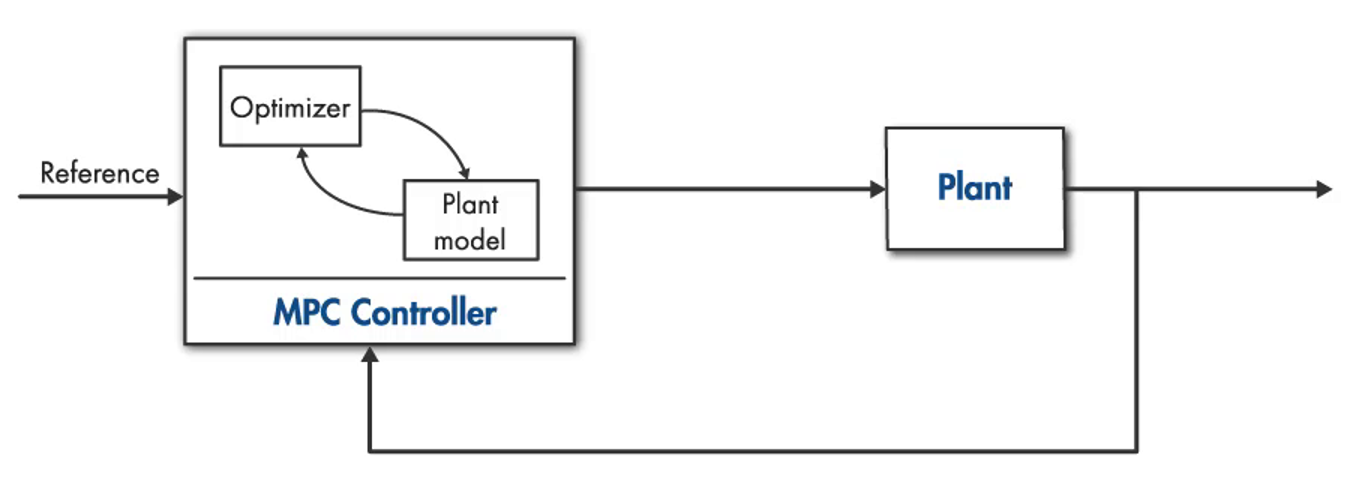
그림 3. 아주 단순화된 MPC의 구조와 제어 대상이 되는 플랜트(plant)

그림 3처럼 MPC 제어기를 보면 내부는 optimizer와 예측을 위한 plant 모델로 구성되어 있는 것을 알 수 있다. MPC 제어기 내부의 plant 모델은 계산 시간을 최소화하기 위해 실제 제어 대상 plant보다 좀 더 단순하게 표현하는 것이 일반적이다. 그리고, optimizer는 비용함수를 최소화하기 위한 최적화 알고리즘이라고 말할 수 있다.

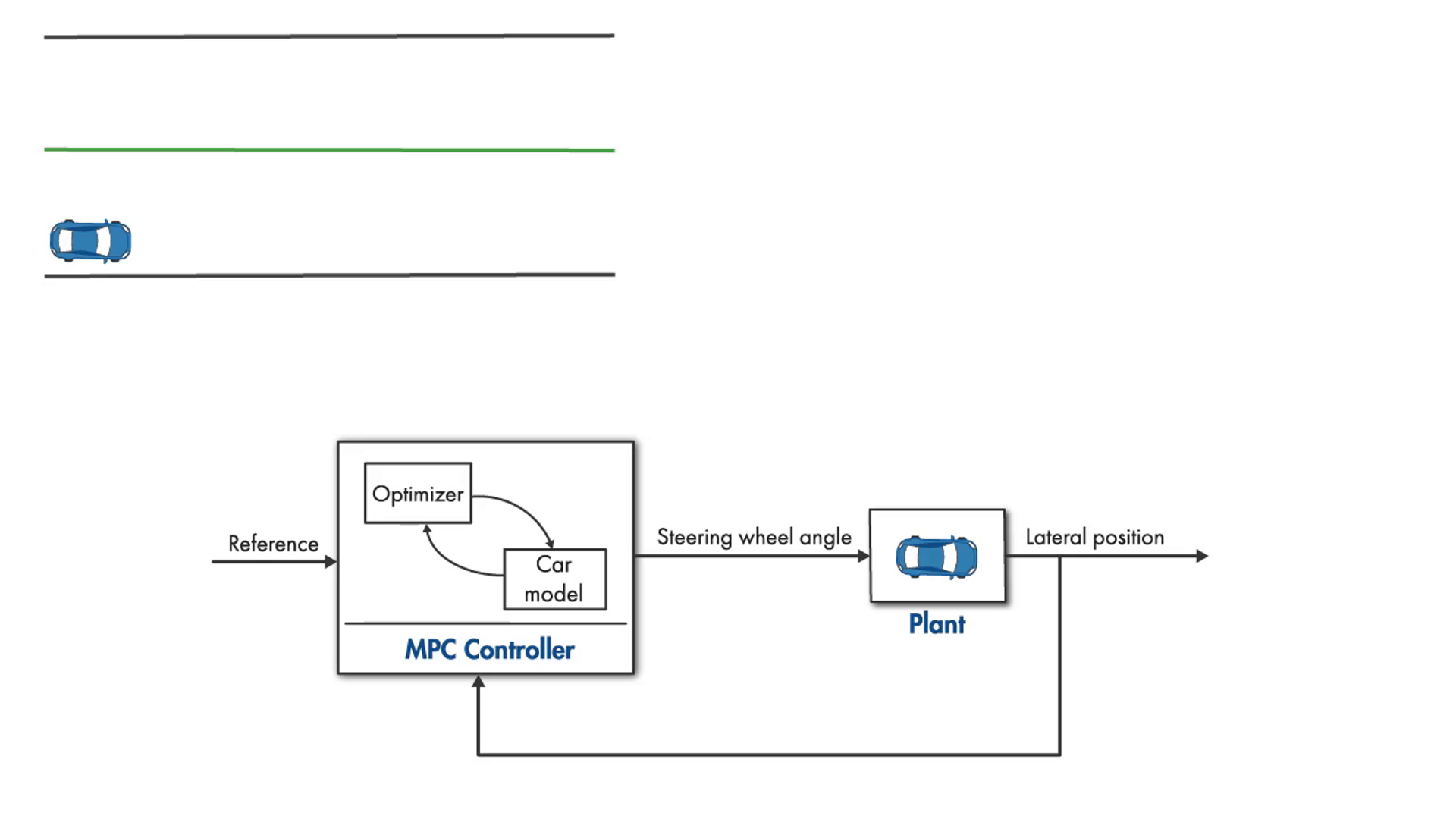
그림 4. 플랜트가 자율주행차인 경우. 초록색으로 표시한 선이 차가 따라가야 할 reference 라인이고, MPC 제어는 reference와 차량중심까지의 거리를 입력으로 받아 조향각을 출력한다.

그림 4에서처럼 제어 대상을 모바일 로봇의 일종인 자율주행차라고 해보자. 이 차를 화면 좌상단의 도로에서 녹색으로 표시된 차선의 중앙을 따라가도록 하려고 한다. 이 차선 중앙이 바로 reference이다. 이제, 제어기의 출력은 차선 중심을 따라가게 하는 조향각 입력이다. 그리고 제어기로의 입력은 조향각 입력에 따라 차량이 움직여 바뀌고 있는 차선 중심에서부터 차량 중심까지의 거리인 횡방향 위치(lateral position)이다.

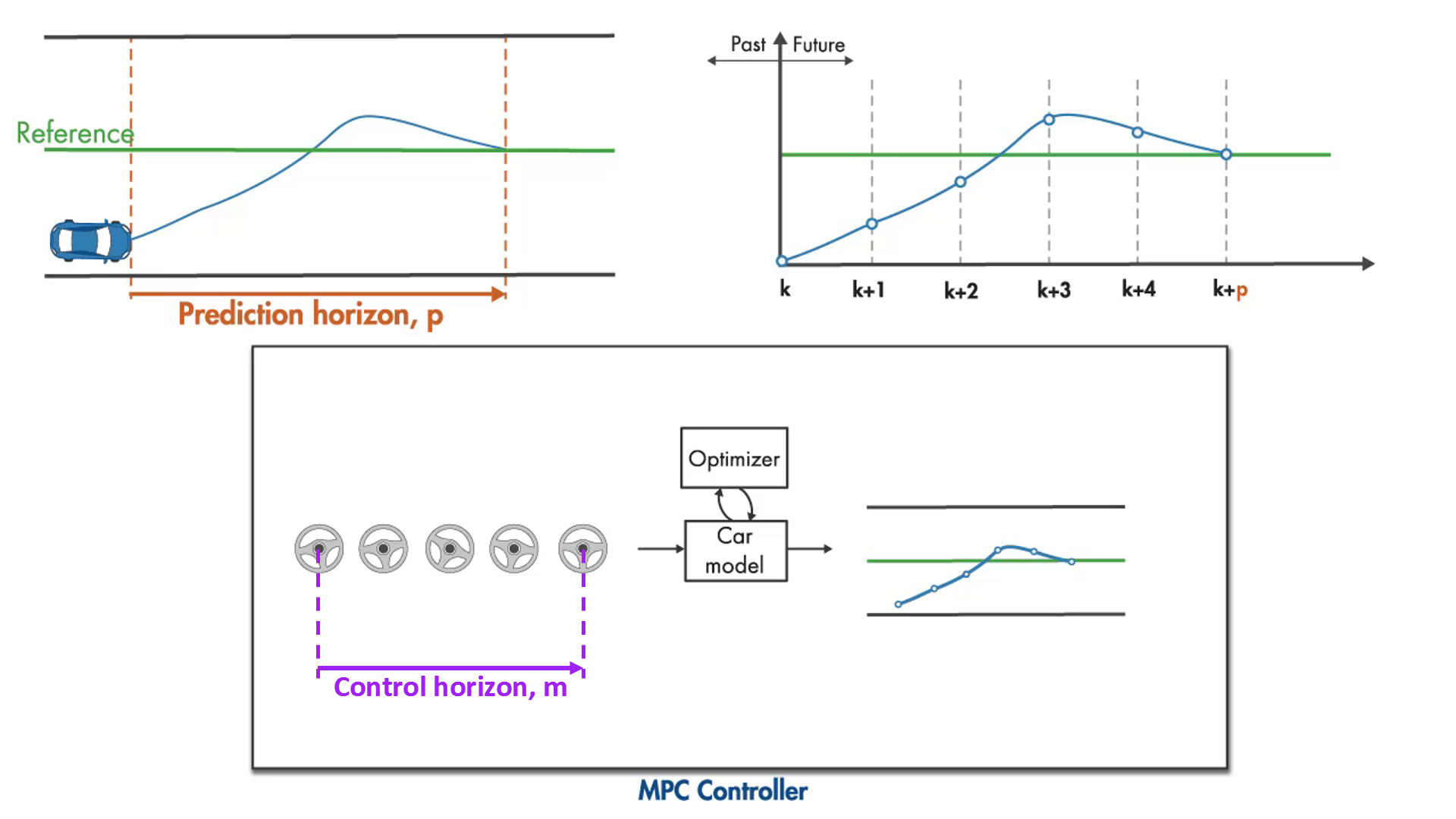
그림 5. 임의의 최초 제어 입력과 prediction horizon

그럼, 그림 5에서 처럼 최초 제어 입력을 만들어 보자. 이 때, 몇 번의 time step 동안에 대한 제어입력을 계획할지를 설정할 수 있는데 이 기간을 control horizon(보라색으로 표시)이라고 한다. 이렇게 지정한 임의의 초기 제어 입력과 차량의 거동예측 모델을 사용하면 일정 time step 이후에 내 로봇이 어디에 존재하는지 예측할 수 있다. 이로써 예측되게 되는 plant의 시간 범위를 prediction horizon(주황색으로 표시)이라고 한다.

그러면, 그림 5에서와 같이 예측된 거동에 대해 optimizer는 비용을 계산할 수 있게 된다. 이 예제에서 비용은 크게 두가지로 구성한다. 첫 번째 비용 요소는 각 시간 단계에서 reference와의 횡방향 오차이다. 이것은 그림 6에서 보는 것과 같이 설명할 수 있다.

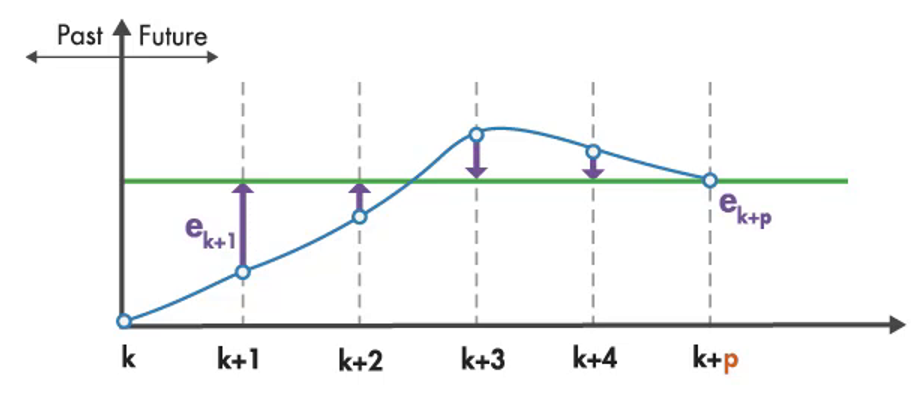
그림 6. reference와의 횡방향 오차

그리고 두 번째 비용 요소는 control horizon의 조향 입력의 변화량인 $\Delta U$이다. 다시 말하면, 제어를 위해 노력한 양을 두 번째 비용으로 삼는것이다.

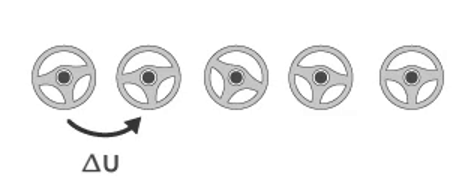
그림 7. 조향 입력의 변화

이 둘을 이용하면 최종적으로 아래 그림 8과 같이 비용함수를 구성할 수 있게 된다. 이렇게 되면 각 단계에서 최소한의 노력으로 최대한 빨리 그리고 안정적으로 횡방향 오차를 줄일 수 있게 된다.

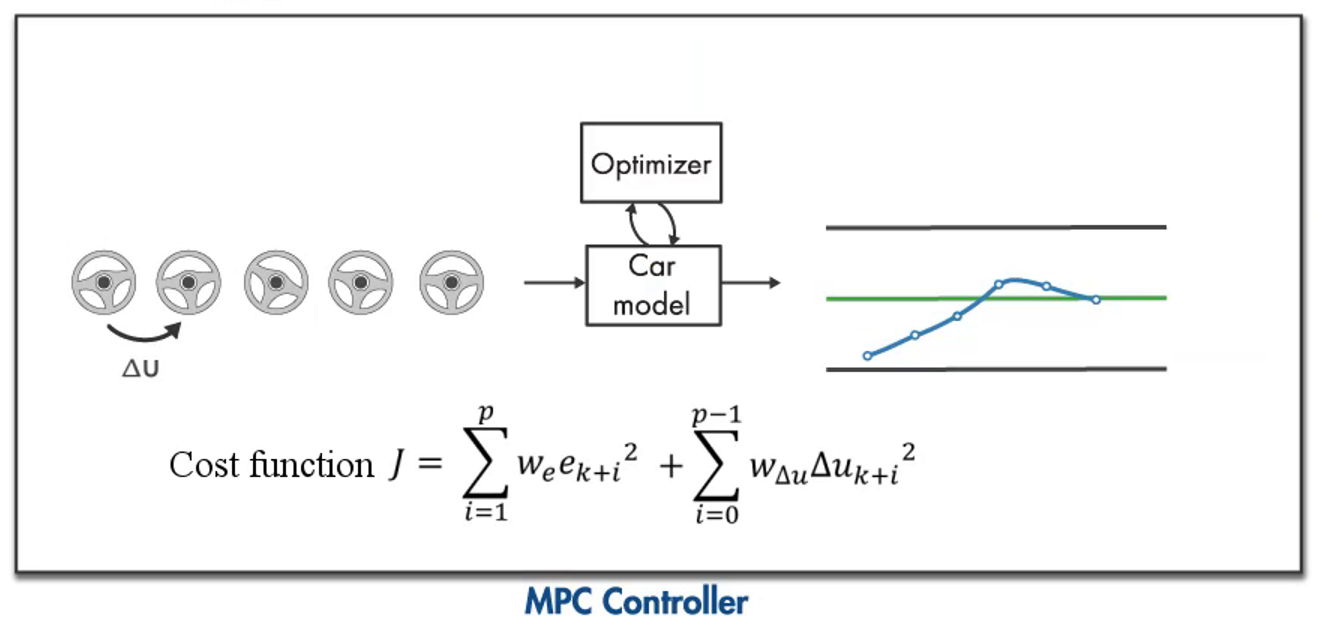
그림 8. MPC 제어기의 목적 함수 선정 예시

그래서, 초기 입력에 대한 비용값을 계산한 값이 50이라고 하면 Optimizer에서는 이 비용함수를 최소화할 수 있도록 최적화 솔버를 이용하여 더 나은 값을 찾기 위해 계속 계산을 진행한다. 두번째는 비용값이 45로 줄었으며, 한번 더 계산을 진행하였더니 비용값이 20이 될 수 있을 것이다.

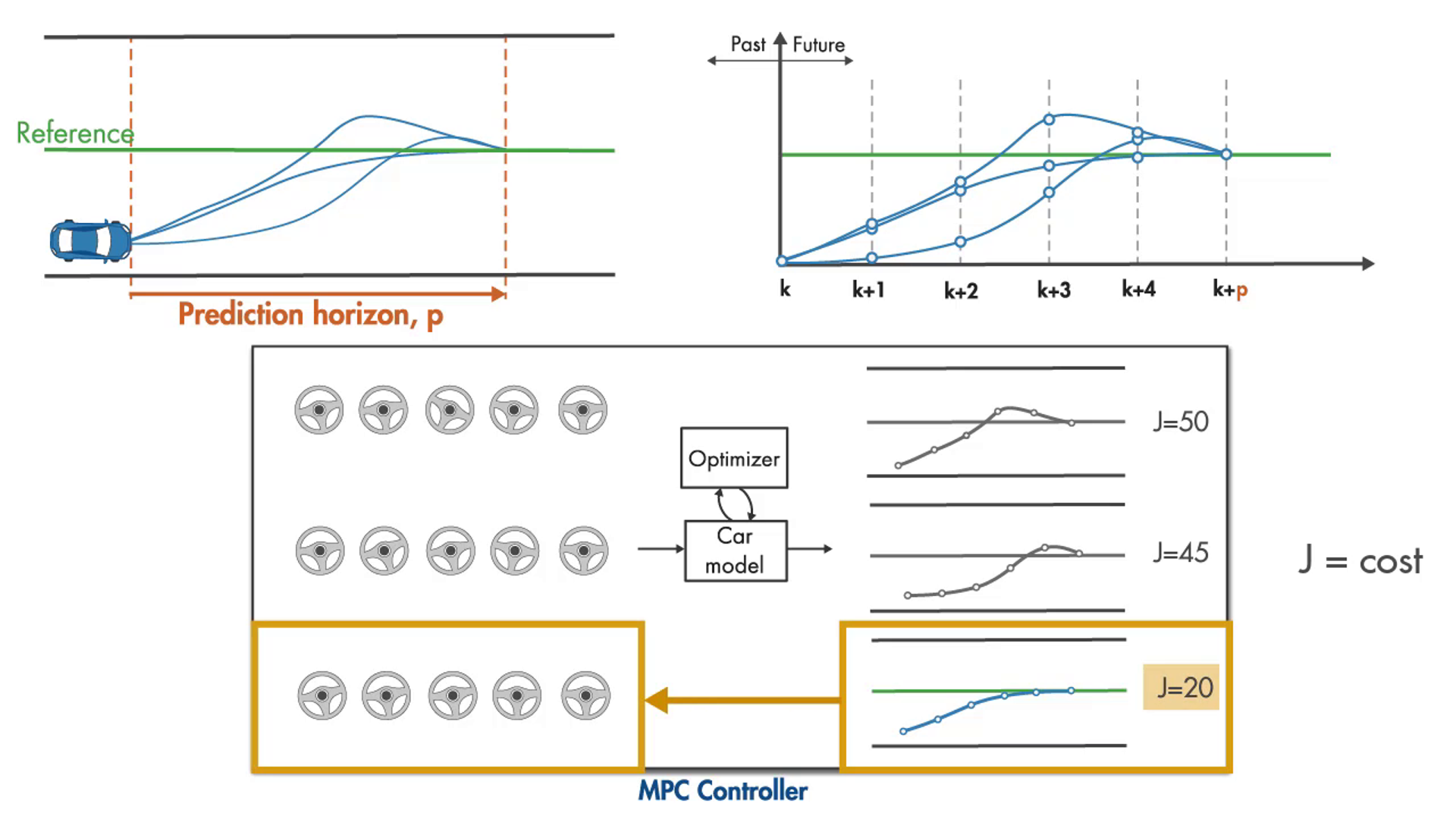
그림 9. MPC 제어기의 목적함수 최적화를 통한 경로 수정 예시

계산을 이렇게 계속하다보면, 몇가지 기준에 따르는 솔버 종료조건에 따라 더 이상 비용을 줄이기 어려운 최적 제어 값이 얻어지고 제어기는 이 제어 입력을 최종적으로 출력하게 된다.

Why use MPC?

그렇다면 어떤 이유로 MPC를 사용하는 것일까?

Preview Capability

첫번째로, 이름 그대로 prediction이 가능하다. 미래의 거동을 고려한 제어 입력으로 장기적으로 시스템을 안정되게 제어할 수 있다.

Control of MIMO Systems & Coupled Dynamics

두 번째로, MIMO 시스템을 제어할 수 있다. 모바일 로봇이 만약 매우 빠른 속도로 이동한다면, 조향입력이 커질 때는 속도를 낮춰야만 안정되게 곡선 경로를 추종할 수 있기 때문에 종방향과 횡방향 제어를 동시에 고려해야 한다. 다시 말해, 빠른 속도로 이동하는 로봇 중 하나인 자율주행 등에 적합한 제어 방식이다.

Multiple control objectives

셋째로, 다수의 제어 목표를 고려할 수 있다. 정해진 경로를 최대한 벗어나지 않으면서도, 주행 안정성을 보장하고, 외부 물체와의 충돌도 고려하는 등 비용함수의 어떻게 조합하느냐에 따라 여러 제어 목표를 한번에 고려하는 제어입력을 생성할 수 있다.

Dynamically feasible planning

네 번째로, 내부에 로봇의 거동 예측 모델을 사용함으로써, 동역학적으로 추종가능한 계획을 수립할 수 있다.

Constraints of inputs, outputs, states

마지막으로는, 입력, 출력, 혹은 시스템의 예측 상태에 대해 제약조건 준수하도록 할 수 있다는 장점도 있다.

Two approachese for the path tracking

그럼 왜 MPC는 모델 예측 제어라는 이름을 가진 제어기 인데 path planner로 사용된다고 얘기하는 것일까?

One-Level

만약, MPC 제어기에 로봇의 위치와 목표 위치를 제공해서 목표위치에 도달할 때까지의 waypoint들을 출력하도록 하거나 시간에 따른 속도/조향각 등의 제어명령을 출력하게 MPC 제어기를 구성하면 global path planner로서 mpc를 사용하는 것이 된다.

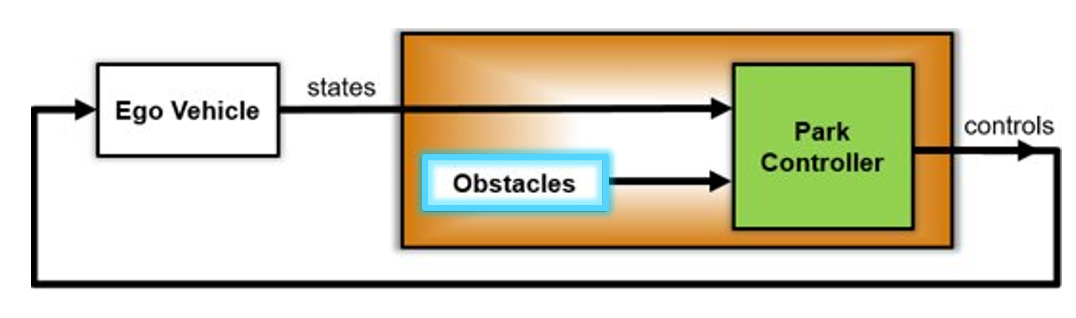
그림 10. MPC를 이용해 Global path planner로 사용하는 경우

이 때, 주변 장애물 정보를 제공하고 이 장애물과의 거리가 음수가 되지 않게 제약조건을 구성하면 장애물과의 충돌을 회피하는 경로를 생성할 수 있다.

하지만, 이 방법은 최적화 해법이 초기치에 민감하다는 점을 고려하면 문제가 복잡해지는 경우, 해가 수렴하지 않고 적절한 경로를 얻어내지 못할 수도 있다.

Two-Level

첫 번째 포스팅에서 언급했던 것처럼 Path planning을 하는 시점에서 모든 정보를 알수도 없고, 복잡한 실제 환경에서의 path planning을 수행하기 위해 일반적으로 global path planning과 local path planning의 조합인 계층구조적인 path planner를 사용하게 된다.

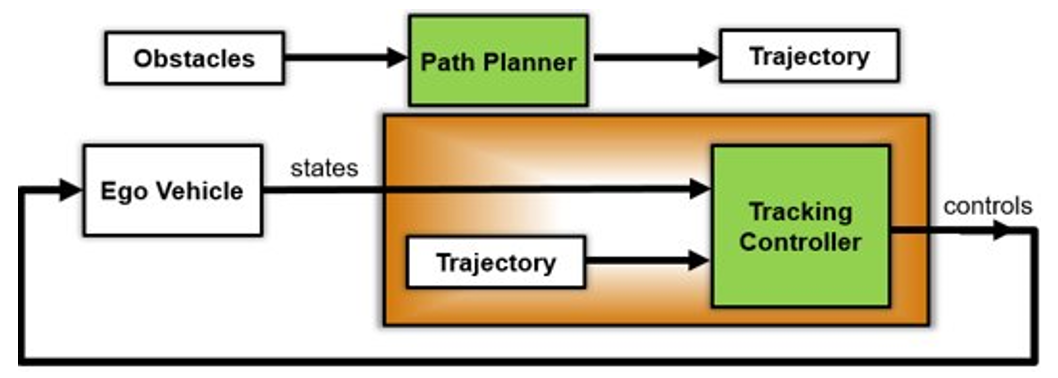
그림 11. Global path planner를 사용하여 생성한 경로를 MPC가 추종하도록 2단계로 설계하는 경우

만약 그림 11과 같이 탐색 기반 혹은 샘플링 기반의 global path planner를 사용하여 생성한 경로를 추종하도록 MPC를 설계한다면 이전 단계에서 생성된 경로가 MPC 제어기의 초기치 역할을 하여 계산 속도도 빠르고 안정적으로 수렴하는데 도움이 된다. 이를 통해 초기 경로계획 시점에서 고려하지 못한 주변 물체와의 충돌도 피하면서 부드러우면서도 안정적으로 로봇을 제어할 수 있는 최적 경로를 얻어낼 수 있다.

Ex) Truck-trailer Reverse Parking: NLMPC Formulation

예를 들어 아래 그림 12에서와 같이 trailer가 달린 트럭을 후진주차 하는 경로를 생성하는 문제에 대해, MPC가 global path planner 자체로 사용되는 경우와 global path planner는 탐색 기반 혹은 샘플링 기반으로 만들고 이를 MPC가 추종하는 경우를 각각 알아보도록 하자.

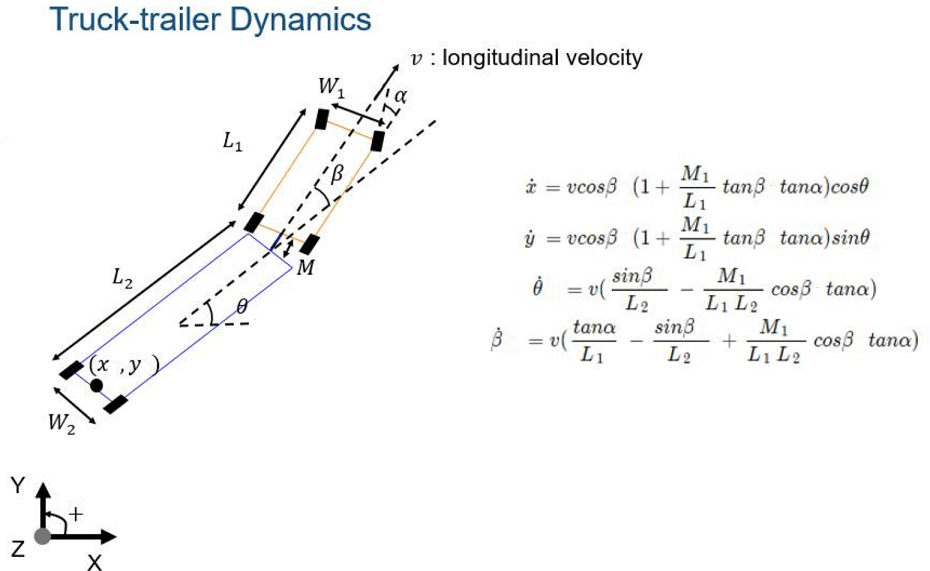
그림 12. trailer가 달린 트럭의 kinematics
출처: MathWorks

우선, Truck-trailer 모델이 필요하다. 일반적인 모바일 로봇보다는 훨씬 복잡한 kinematics를 가지고 있는 것을 알 수 있다. 두 바디 사이의 관계를 수식화하고 이를 state space 형태로 모델링하면 그림 12의 오른쪽과 같다.

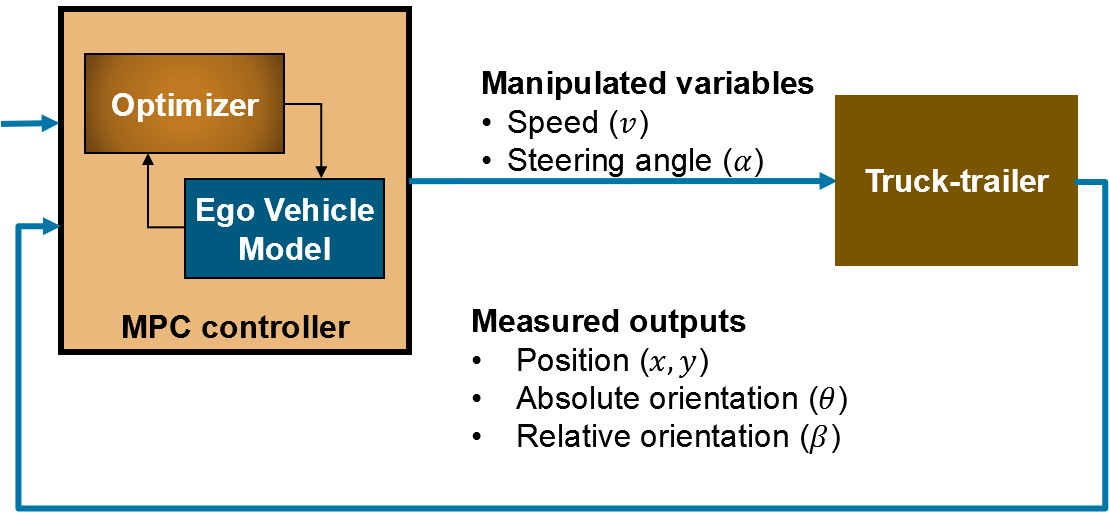
그림 13. MPC 제어기를 이용한 제어 구조

MPC 제어기의 입출력 및 전반적인 제어 구조는 그림 13과 같다. 예측 모델에서 현재 상태는 차량의 위치와 각 바디의 방위각을 입력받아 계산하고, 최종적으로 제어기가 출력하는 명령은 속도와 조향각으로 설정한다. 아래 식 (1)의 one level 모델의 비용함수를 보면, 현재의 pose와 목표 주차 상태의 pose 사이의 차이가 최소화되도록 구성한 것을 알 수 있다.

\[\text{minimize: } \quad \quad \quad \quad \quad \quad \quad \quad \\ w_1|s(d)-s_{target}|^2\]

이 때, 제약조건으로 주변 물체와 일정 수준 이상의 안전거리를 유지해야하며, 속도는 안전을 위해 후진 vmin, 전진 vmax 범위로 유지하고, 가속도는 제어의 안정성을 위해 특정 가속도 범위 이내로 유지하도록 정의하였다.

\[\text{subject to:} \quad \quad \quad \quad \quad \quad \quad \quad \\ \text{dist}_{obstacles} \geq \text{dist}_{safe} \\v_{min}\leq v \leq v_{max}\\ \alpha_{min}\leq\alpha\leq\alpha_{max}\]

만약 global path planner를 사용해서 기준 경로를 외부에서 입력받았을 때는 어떻게 문제가 달라질 수 있을까? 이렇게 비용함수를 변경할 수 있을 것이다.

\[\text{minimize: } \quad \quad \quad \quad \quad \quad \quad \quad \\ \int_{0}^{d}\left(w_1|s(t)-s_{ref}|^2 + w_2|\Delta u(t)|^2\right)dt\]

Global path planner에서 생성된 경로는 $s_{ref}$로 위치와 방위로 구성된 목적지까지의 waypoint 형태로 입력된다. 따라서, 시작부터 종료까지 경로상의 waypoint와의 pose 차이를 모두 더한 비용과 이를 이행하기 위해 만들어지는 제어 명령들 $\Delta u(t)$의 크기를 모두 더함으로써 최소 노력으로 정해진 경로를 최대한 따라가는 경로가 구성되게 된다.

그림 14에서처럼 먼저 one level MPC 제어기의 경우를 보면, 그림 상에 시작pose와 목표 pose가 붉은색 x 로 표기 되어 있고 제어가 완료될때까지 충돌없이 전체 경로가 구성되어 목표지점에 도달하는 것이 보인다.

그림 14. One-level MPC 제어기를 이용한 Truck-trailer Reverse Parking

다음으로 그림 15에서처럼럼 two level mpc 제어기의 경우 검은색으로 global path planner의 결과 경로가 입력되어 이를 잘 추종하도록 차량이 제어되는 것이 보인다.

같은 환경에서 초기조건이 달라서, 경로가 조금 더 복잡한 형태의 문제를 보여주고 있는데 앞서 언급한 바와 같이 two-level mpc controller가 좀 더 짧은 시간안에 안정적으로 경로를 생성할 수 있기 때문이다.

그림 15. Two-level MPC 제어기를 이용한 Truck-trailer Reverse Parking

Model Predictive Control Toolbox

Key featuers of Model Predictive Control Toolbox

그림 16. MATLAB의 Model Predictive Control Toolbox 소개 페이지

MATLAB에서는 Model Predictive Control Toolbox를 통해 MPC 제어기의 구현을 돕고 있다.

다양한 형태의 MPC 문제를 구성하기 위한 MATLAB 함수나 Simulink block을 제공하고 있고, MPC 문제를 구성하고 나면, 시뮬레이션을 통해 설계한 MPC의 성능을 검증할 수 있다.
이 때 제공하는 함수나 블록에서 생성한 코드는 ISO 26262나 MISRA와 같은 여러 standard를 만족한다.
MPC의 계산을 위해 제품에 포함된 여러가지 솔버를 적용할 수 있으며 Forces pro와 같은 외부 third party MPC 솔버를 사용하여 simulation 하거나 코드 생성할 수 있다.
마지막으로, 시뮬레이션을 통해 검증된 MPC 제어기는 C나 C++ 형태의 코드로 코드 생성하여 임베디드 시스템에 실장할 수 있다.

Types of MPC

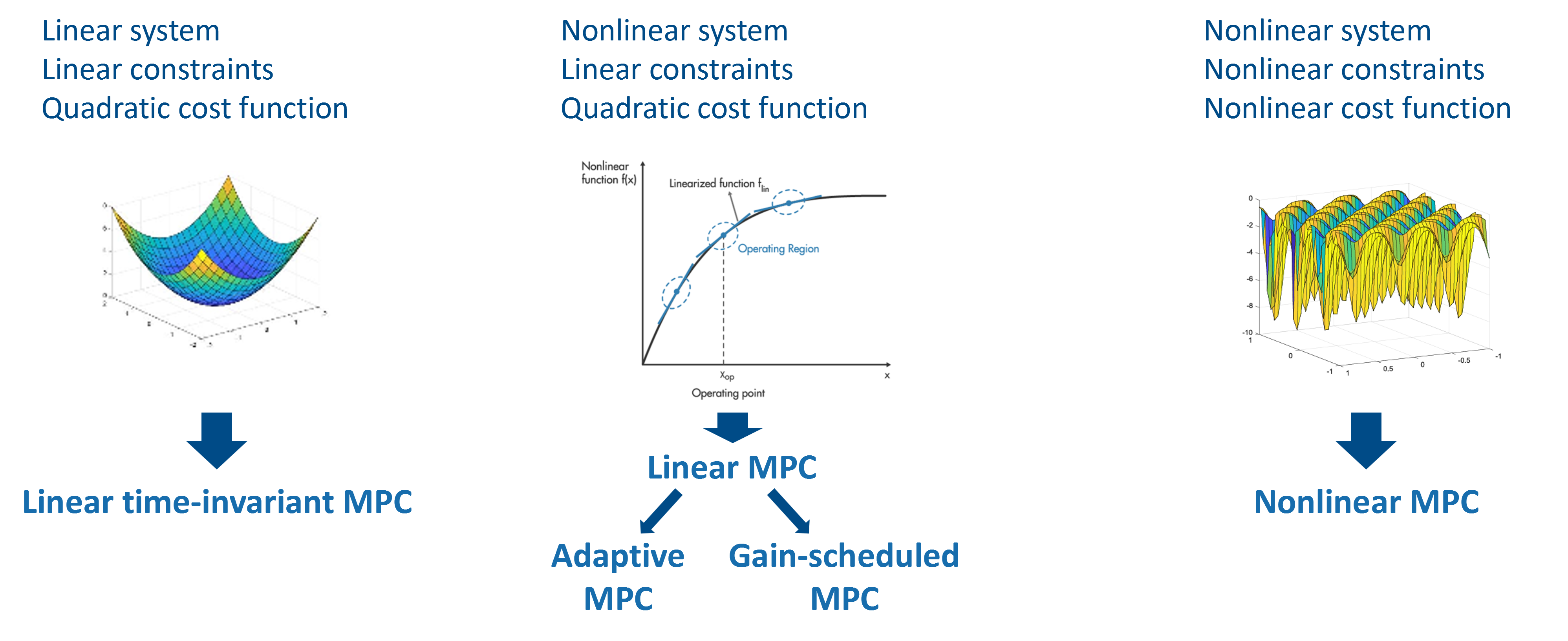
그림 17. 다양한 타입의 MPC 문제

MPC는 (1) system model, constraint, cost function의 형태에 따라 Linear system, linear constraint, quadratic 형태의 cost function을 가지면 linear MPC 문제, (2) 다른 조건들은 동일하나 nonlinear system인 문제의 경우 각 구간별로 system model을 선형화하여 사용하는 adaptive MPC 혹은 gain-scheduled MPC 문제 (3) system model,constraint, cost function이 모두 비선형인 경우 Nonlinear mpc 문제를 풀게 된다.

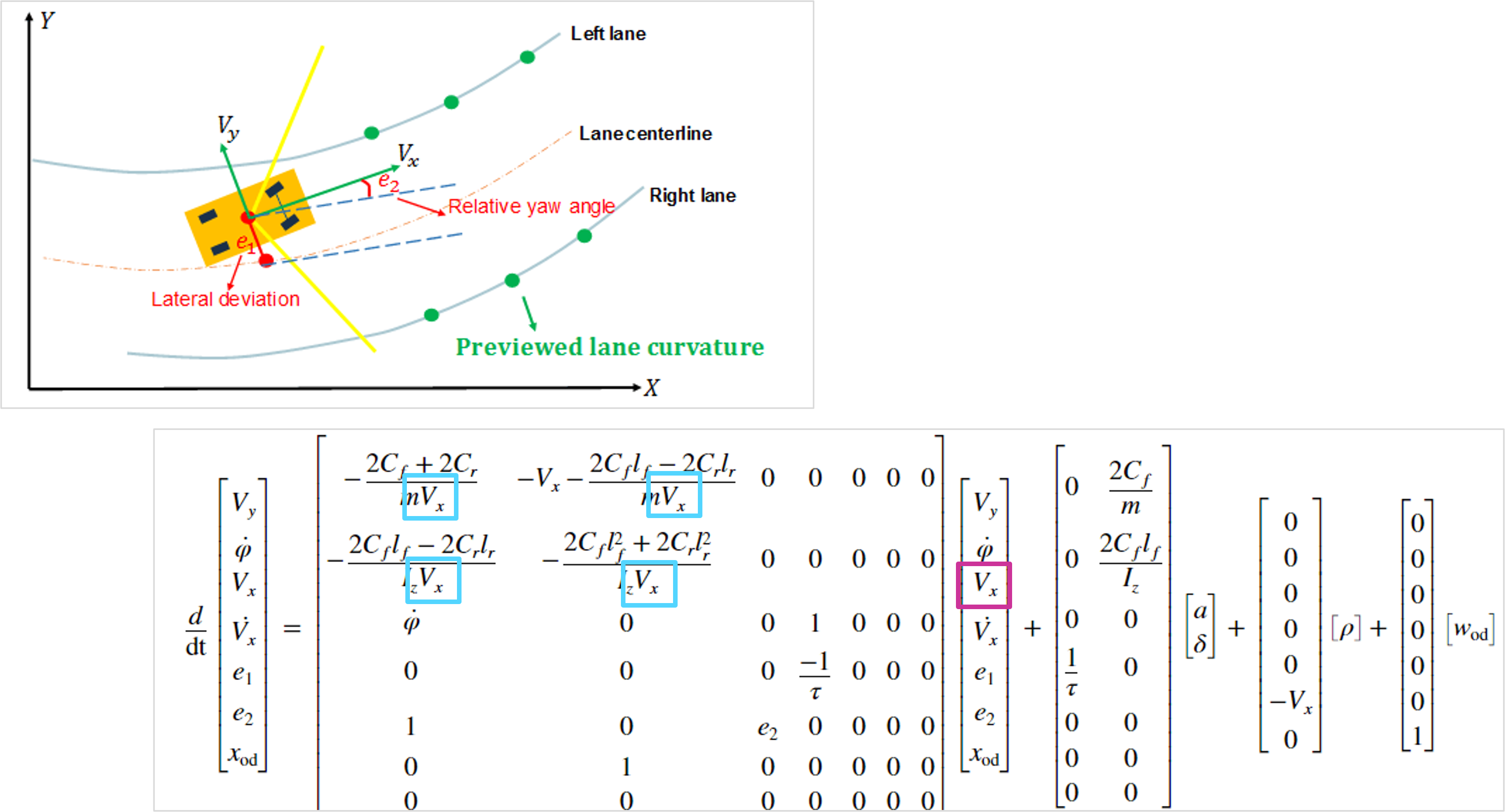
그림 18. 비선형 MPC를 적용해야하는 자율주행 어플리케이션의 예시

만약 가장 풀이가 쉬운 linear mpc 부터 적용하여 제어기가 목표 성능을 만족하지 못하면 더 복잡한 형태의 mpc를 사용할 수 있다.

예를 들어 차선 중심을 따라가는 이런 자율주행차를 제어하기 위해 그림 18과 같은 모델을 사용한다면 보이는 것과 같이 system model에도 종방향 속도가 있고, state에도 종방향 속도가 있어 수렴을 위해 매 스텝 계산할 때마다 system model이 변경되는 비선형 모델이 된다.

만약 속도가 낮고,속도의 변화가 크지 않은 로봇 청소기와 같은 모델이라면 linear MPC를 사용할 수 있고, 속도의 운용범위가 넓은 시스템이라도 속도의 변화가 크지 않다면 adaptive mpc를 사용할 수 있다. 하지만, 자율주행 시스템과 같이 속도의 변화가 크고 운용범위가 넓고, 장애물까지 고려하는 비선형 constraint까지 있다면 nonlinear MPC를 사용해야 한다. MPC Toolbox에서는 이와 같은 다양한 형태의 MPC를 거의 다 지원하고 있지만 그 중에서 nonlinear MPC를 적용하는데 있어 어떤 장점이 있는지 좀 더 자세히 알아보자.

Nonlinear MPC

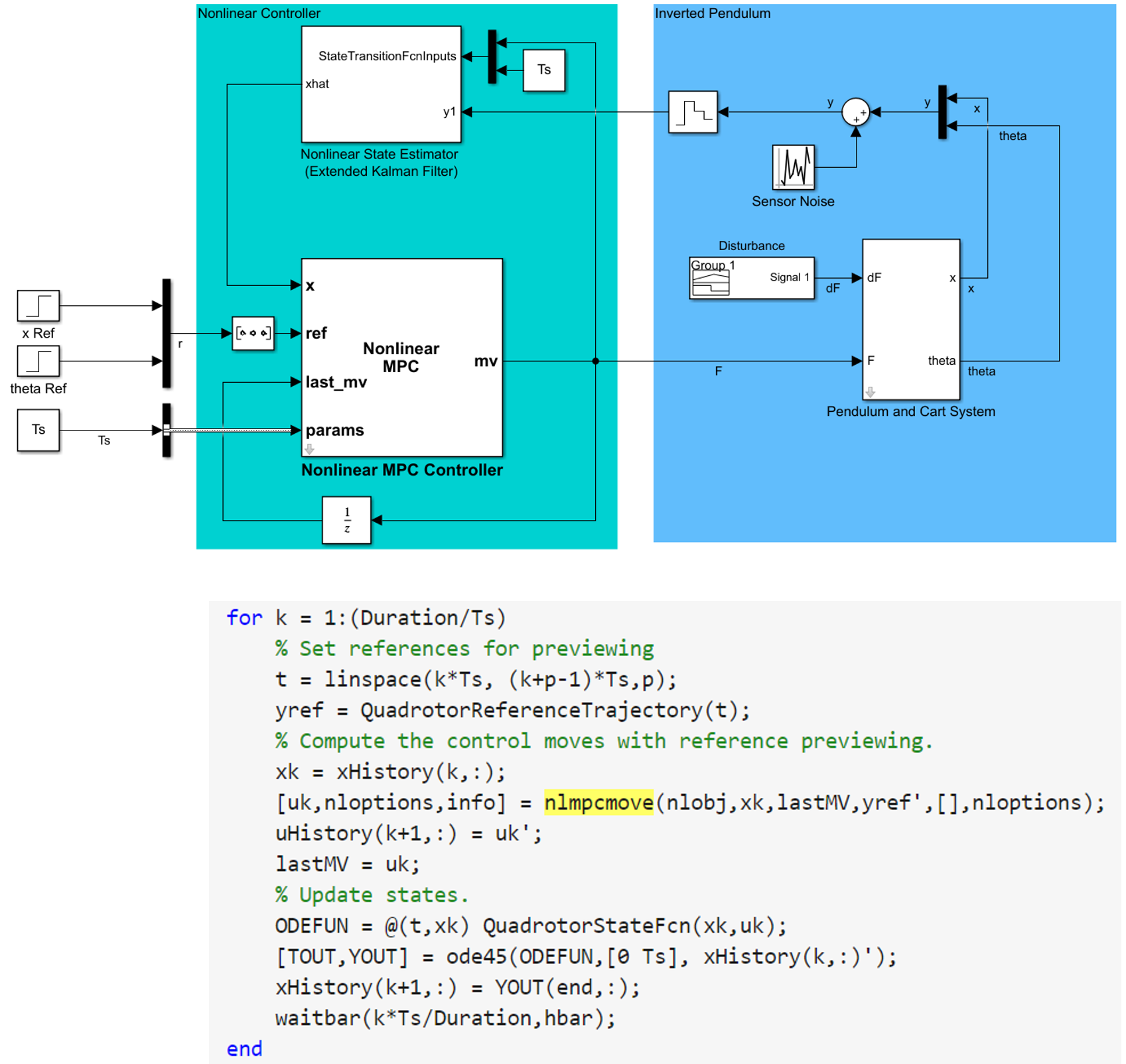
그림 19. Nonlinear MPC 기능으로 제공되는 블록 혹은 함수의 사용 예예

MPC Toolbox에서 제공하는 Nonlinear MPC 함수 혹은 block은 Optimization Toolbox에서 제공하는 SQP 알고리즘 일종인 fmincon을 사용하여 비선형해를 얻는다. 그리고, 다른 여러 MPC 기능과 동일하게 nonlinear mpc의 경우에도 C/C++ 형태의 코드를 생성하여 임베디드 보드에 실장할 수 있다.

Multi-stage nonlinear MPC

그림 20. Multi-stage nonlinear MPC 제어기를 이용한 Truck-trailer Reverse Parking

이러한 nonlinear mpc 중에서도 최근에 출시된 기능 중에 multi stage nonlinear mpc는 각 time step에서 비용함수와 constraint 함수를 구분하여 지정할 수 있어 매 time step 마다 주변 환경이 다이나믹하게 변경되는 모바일 로봇의 경로 계획 및 제어 문제에 아주 편리하게 적용할 수 있다.

그림 20의의 예제에서는 tailer를 가진 truck의 후진 주차 경로 생성 문제를 푸는데 있어 40개의 time step을 지정하여 각 time step마다 cost function과 cost function Jacobian을 따로 지정하여 매 순간 이동하는 동적인 장애물의 위치를 변경 적용하거나 로봇과 가까운 물체에 대해서만 고려를 할 수 있음을 보여준다.

만약, multi stage mpc가 아닌 경우에는, 전체 time step을을 관통하는 cost function이나 constraint function을 수식화하여야 하기 때문에 구현의 복잡도가 높아지게 된다.

그리고 이때, 경사하강법 기반의 수치해석적인 솔버를 사용하기 때문에 cost function혹은 constraint function에 대한 1차 편미분 형태인 Jacobian 함수를 필요로 하는데 수식적으로 구현하기 어려운 이 Jacobian 함수도 automatic differentiation 함수를 이용해 자동으로 구성해준다.

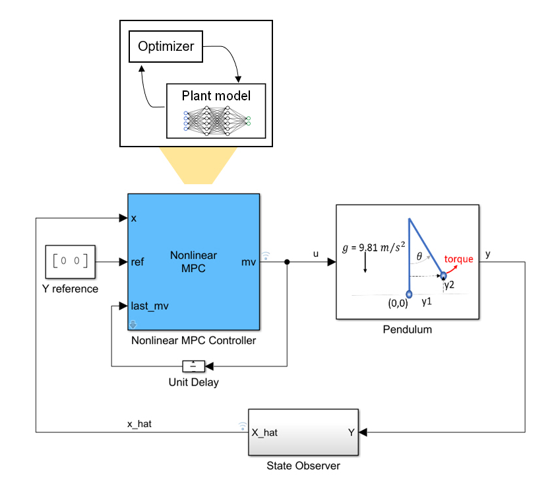
그림 21. Nonlinear MPC의 system matrix를 뉴럴넷으로 대체하는 것 또한 가능하다.

또, 경우에 따라 system matrix를 구현하기 어려울 때, multi stage nonlinear mpc 문제를 위한 system matrix를 딥러닝 neural network를 이용하여 외부에서 학습한 후 mpc에 적용할 수도 있다. 여기에 대한 Jacobian matrix도 역시나 자동으로 계산되며, 코드 생성도 지원된다.

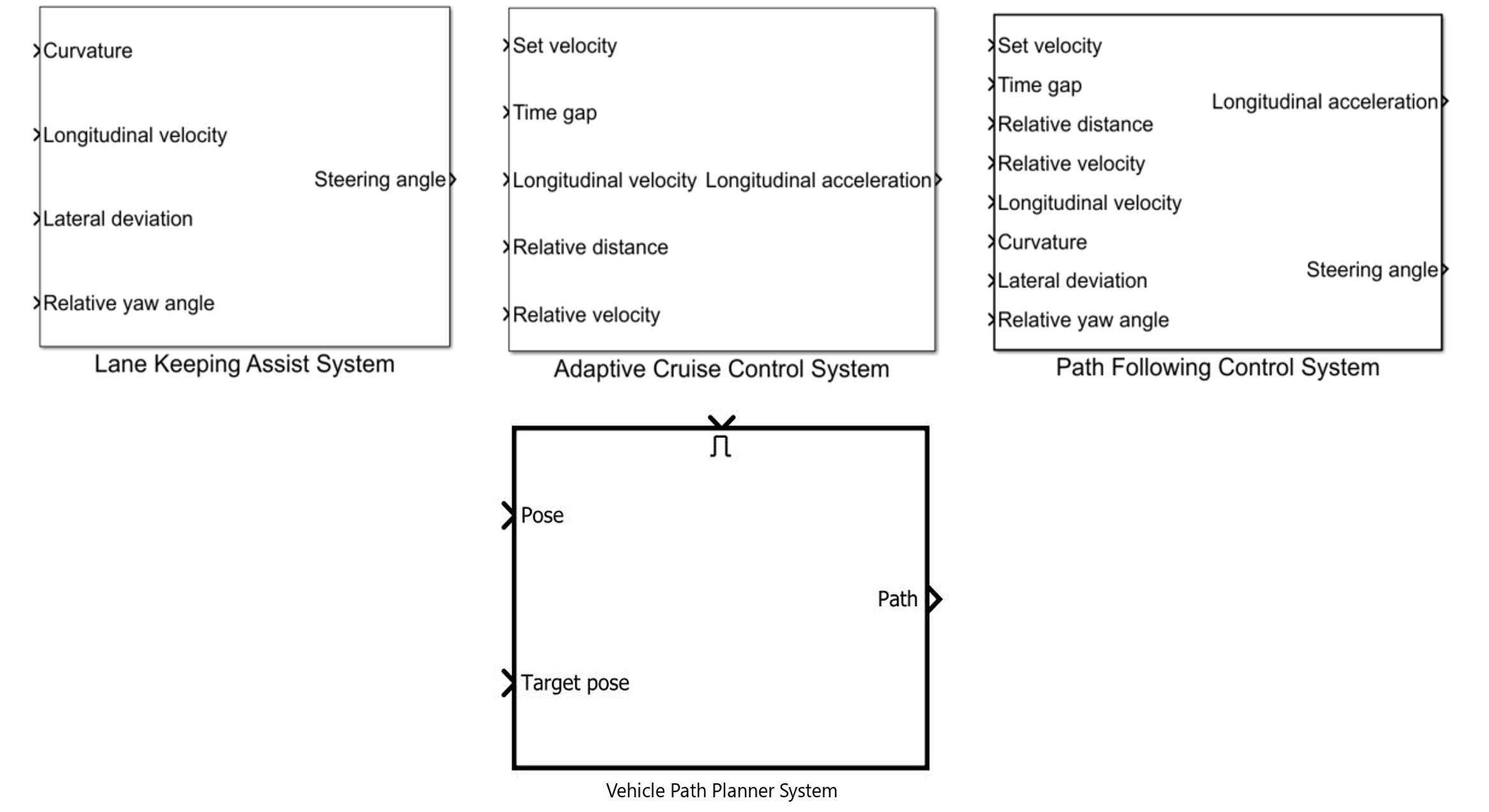
그림 22. 자동차 어플리케이션에 특화된 MPC 블록

그리고, 자동차 관련 특정 application에 대해서는 그림과 같이 이미 완성되어 있는 블록을 제공하고 코드 생성을 지원한다. 현재 지원하는 application은 lane keeping, adaptive cruise control, 그리고 이둘을 합한 path following control system, 그리고 주차 시스템을 위한 vehicle path planner가 있다.

그림 23. MPC를 이용한 자동차 어플리케이션 예시

Technical Resources

이번 시간에는 MPC 에 대해 알아보았다. Path Planning 분야 외의 로봇 개발을 위한 다른 내용이 궁금하다면 아래의 매스웍스 코리아에서 제공하는 모바일 로봇틱스 그리고 자율주행 웹 포털을 통해 정보를 얻어갈 수 있으니 참고하기 바란다.

MATLAB Mobile Robotics Web Portal

그림 24. MATLAB을 이용한 육상 이동 로봇 개발 Web Portal (링크)

MATLAB ADAS Web Portal

그림 25. MATLAB을 이용한 자율주행/ADAS 개발 Web Portal (링크)

MATLAB Onramp Series

매트랩 기초 사용법을 학습하고 싶은 경우 MathWorks 홈페이지 내의 Onramp 라는 무료 트레이닝 코스를 활용할 수 있다. Onramp는 웹상으로 진행하는 온라인 무료 교육으로, 컴퓨터에 매트랩을 설치 할 필요 없이 온라인으로 매트랩 관련된 여러 기초 내용을 학습할 수 있다.

그림 26. MATLAB을 무료로 배울 수 있는 Onramp 시리즈 (링크)